[Column] Il Nuovo Mondo – Giugno 2016

I segreti della disinformazione – Sesta puntata

La presentazione dei dati

Un paio di puntate fa abbiamo visto come si possa utilizzare la rappresentazione grafica di dati per sostenere una determinata tesi, ovvero dimostrare una qualche correlazione fra due fenomeni apparentemente indipendenti. Un caso tipico è l’improbabile teoria che sostiene che il consumo pro capite di formaggio negli Stati Uniti sia la causa principale dei decessi per soffocamento durante il sonno, il tutto a partire dai dati forniti dal Dipartimento dell’Agricoltura americano. Osservando il grafico risultante verrebbe effettivamente da pensare che una tale dipendenza esista davvero, anche perché il fattore di correlazione è superiore al 94%, quindi ben più elevato che in altre situazioni in cui si sa esserci effettivamente una connessione fra due diversi fenomeni.

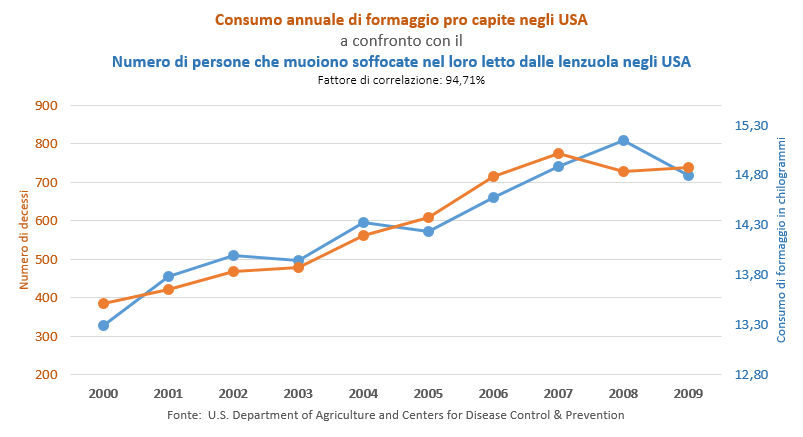
Ma questo cosa significa allora, che non possiamo più fidarci neppure dei dati oggettivi che provengono da fonti certe e affidabili? In realtà no. Il problema nasce da un equivoco di fondo, ovvero dall’assumere che l’analisi dei dati da sola possa essere effettivamente sufficiente a sostenere una tesi. È quello che succede quando si imita il modo in cui la scienza presenta e sostiene le proprie teorie, senza comprenderne a fondo metodo e processi.

In una ricerca, infatti, misurazioni e dati entrano in gioco in due fasi differenti.
Nella prima, una potenziale correlazione fra dati viene utilizzata per sviluppare un’ipotesi di lavoro. Questa viene poi approfondita tramite una serie di esperimenti che possono portare a sviluppare una teoria. Basandosi su quella teoria, si fanno previsioni su quelli che potranno essere i risultati di ulteriori esperimenti fra i quali, possibilmente, uno di falsificazione, ovvero inteso a dimostrare che la teoria è falsa. A quel punto si effettuano gli esperimenti in questione, si raccolgono nuovi dati e li si confrontano con le previsioni iniziali. Sono proprio quest’ultimi dati che in genere vengono presentati negli articoli scientifici a supporto della teoria.

In una strategia di disinformazione, invece, ci si ferma alla prima fase, ovvero si usano i dati che dovrebbero semplicemente essere utilizzati per sviluppare delle ipotesi di lavoro, per sostenere che una teoria, stabilita a priori, sia valida. È così che il consumo di formaggio diventa causa primaria delle morti per soffocamento durante il sonno.

D’altra parte dobbiamo ricordare che la disinformazione non si basa sulla logica e sul ragionamento, ma semmai di questo imita solo l’apparenza: la disinformazione si basa sulla percezione, per cui non solo è importante presentare i dati, ma anche il modo con il quale li si rappresenta — la scelta del tipo di grafico, l’ampiezza del campione, gli intervalli selezionati, la scala degli assi, persino i colori e le dimensioni dei caratteri dei testi — diventa fondamentale per supportare una falsa tesi.

Vediamo alcuni esempi. Premetto che lo scopo di questo articolo non è dimostrare una tesi rispetto a un’altra, ma far vedere come una qualsiasi tesi possa essere sostenuta con convinzione utilizzando dati reali, per quanto assurda possa essere. Utilizzeremo quindi un fenomeno, quello del cambiamento climatico, sul quale si è discusso moltissimo per far vedere come dai soli dati si possa evincere tutto o niente.

Consideriamo la temperatura media della superficie del pianeta Terra nell’ultimo secolo e mezzo, più o meno. I dati sono presi prevalentemente dagli archivi della NASA e da fonti storiche, ma questo adesso non ha molta importanza, dato che si tratta solo di un esempio. L’importante è che siano dati reali, non inventati.

Se osserviamo il grafico è facile rendersi subito conto come ci sia stato un aumento significativo della temperatura della superficie del nostro pianeta dal 1880 al 2011.

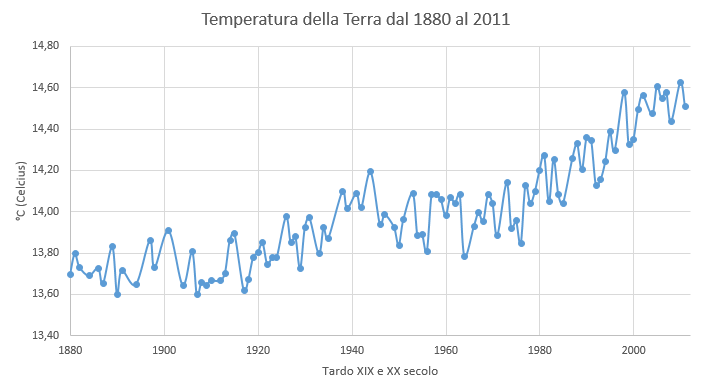
Se poi confrontiamo questi dati con quelli storici a partire dal 1600, sembra evidente come questo incremento sia iniziato proprio verso la fine del XIX secolo, ovvero in piena era industriale, dato che in precedenza la temperatura appare essersi assestata su un valore medio più o meno stabile.

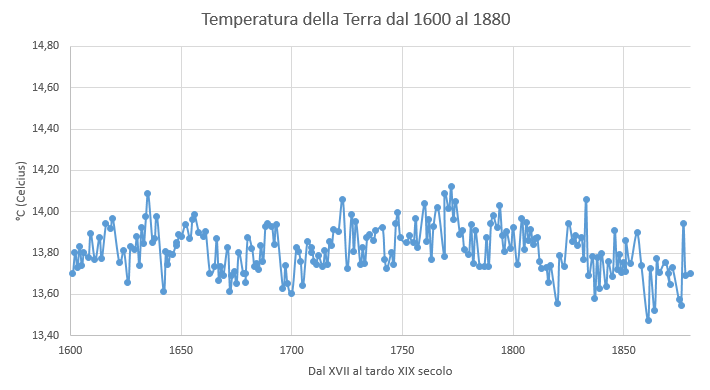
Da qui si possono sviluppare tutta una serie di teorie sulla possibilità che l’avvento dei processi industriali, in gran parte inquinanti, abbia modificato una situazione in precedenza sostanzialmente stabile. Sarà vero? Magari sì, ma non certo perché lo dicono questi dati.

Proviamo infatti ad andare ulteriormente indietro nel tempo. Consideriamo, ad esempio, gli ultimi 11mila anni. Le cose qui si complicano. Quello che sembrava un aumento importante della temperatura quasi scompare rispetto a tutta una serie di aumenti e diminuzioni che si sono verificati nei millenni passati. Non solo: la temperatura attuale è addirittura più bassa di quella che si aveva 10mila anni fa, ovvero nel pieno fiorire dello sviluppo dell’agricoltura e della domesticazione delle specie vegetali.

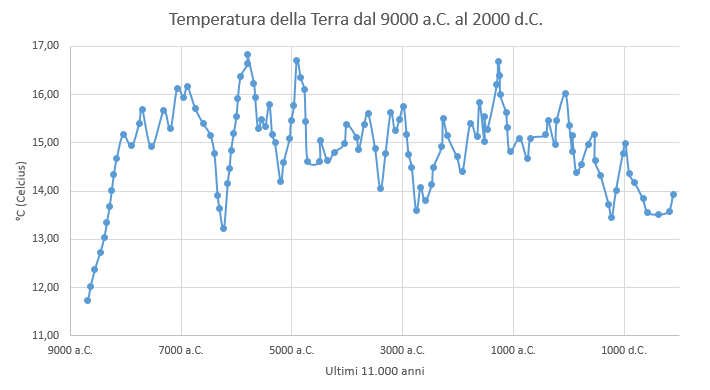
Ecco allora che la teoria antropocentrica perde di forza mentre si apre la strada a tutta una serie di nuove teorie su cui lavorare. Ad esempio, si potrebbe affermare che l’agricoltura fu facilitata da una temperatura maggiore di quella che abbiamo attualmente. Vero? Falso? In realtà non ha molta importanza perché il punto proprio è che non si può affermare qualcosa solo in base a questi dati. A meno, appunto, che non lo si voglia fare in modo strumentale. Ma andiamo ancora più indietro nel tempo. Vi riporto un grafico originale basato su dati ottenuti da fonti differenti, verificati da più ricercatori, quindi sicuramente affidabili.

Riguarda gli ultimi 65 milioni di anni. L’area all’estrema destra, dove c’è la curva di colore rosso, è quella relativa al terzo grafico appena considerato. Praticamente si vede una rapida crescita e poi uno stabilizzarsi della temperatura. Tutte quelle variazioni che ci preoccupavano tanto, risultano del tutto irrilevanti rispetto a quanto è successo nelle epoche passate. Tenete presente che il grafico ha cinque assi orizzontali, uno per ogni sezione, con scale differenti, per comodità, altrimenti sarebbe stato troppo lungo farlo entrare in una sola pagina.

Solo nel Pleistocene ci sono state variazioni molto più elevate di quelle che stiamo sperimentando ora. Si contano quasi una dozzina di picchi e altrettanti minimi nel periodo intercorso da un milione a 20mila anni fa. Se poi andiamo ulteriormente indietro ecco che la temperatura aumenta in modo impressionante fino a raggiungere un massimo all’inizio dell’Eocene, un periodo particolarmente ricco di vita che vide il dominio dei mammiferi dopo che la maggior parte dei grandi rettili si erano estinti.

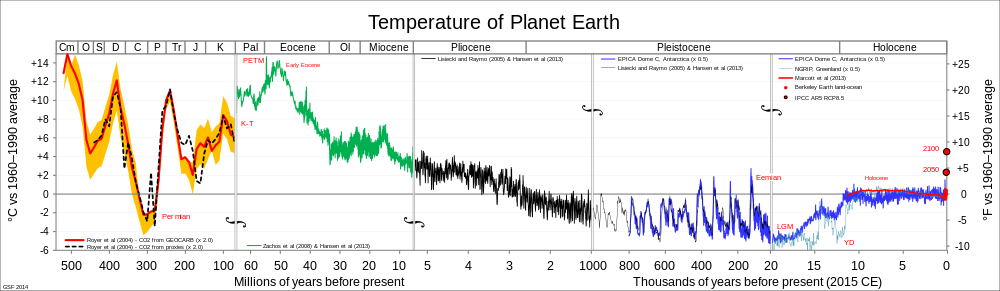
Ma cosa c’entra tutto questo con la disinformazione? Semplice: lavorando su alcuni dei parametri che ci permettono di rappresentare dati, abbiamo ottenuto grafici diversi che ci hanno dato percezioni diverse di un fenomeno e quindi ci hanno permesso di fare affermazioni differenti. Forse alcune di quelle affermazioni sono comunque vere. Forse no, ma sicuramente non è con questi grafici che possiamo stabilirlo. L’analisi di un fenomeno, infatti, si deve basare su un metodo rigoroso e lo studio di molti aspetti differenti di quel fenomeno.

La disinformazione invece gioca su un’opportuna scelta nel rappresentare graficamente solo una parte dei dati disponibili per generare una specifica percezione, e questo può essere fatto anche indipendentemente dai valori numerici. Vediamo come.

Partiamo dalle caratteristiche del grafico su cui possiamo lavorare. La prima è ovviamente il tipo di grafico. Gli stessi dati, rappresentati in modi differenti, possono dare percezioni differenti.

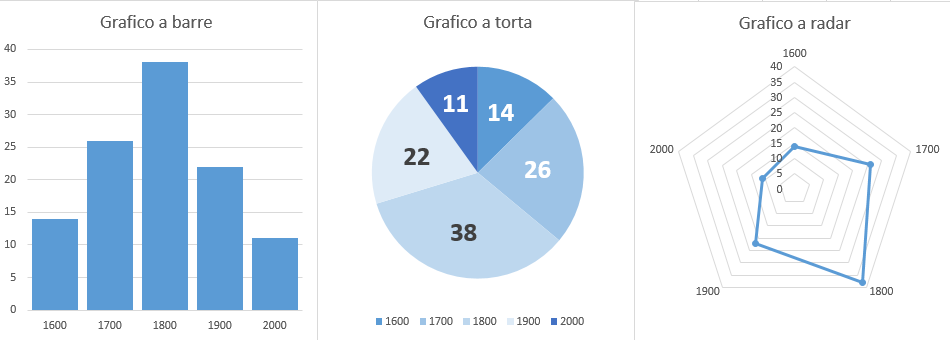
Attenzione: quando parliamo di percezioni non intendiamo necessariamente un’alterazione della nostra comprensione di quali siano i valori in gioco, ma anche aspetti di carattere puramente emotivo. Ad esempio, un picco in un grafico a barre dà un’evidenza forte, positiva o negativa, a seconda della teoria da dimostrare, di uno specifico dato rispetto agli altri valori. Si porta quindi chi lo osserva a ragionare per valori assoluti. Un grafico a torta, invece, porta istintivamente a ragionare per valori relativi anche se i dati non sono forniti in percentuale ma in valore assoluto, come nell’esempio sopra. Questo perché oltre al dato, l’occhio ragiona sulla larghezza delle varie fette. Se poi il dato non viene neppure riportato, tanto meglio.

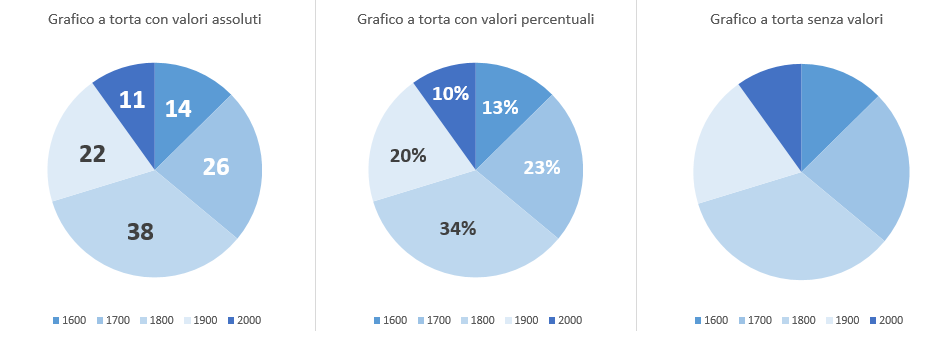
Un grafico a radar porta a ragionare per scostamenti, o se si vuole, per deviazione dalla norma, dove la norma è rappresentata da una distribuzione uniforme radiale dei dati. Utile quando si vuole evidenziare una presunta anomalia. Tenete presente che i valori dei dati nei tre grafici riportati sopra sono sempre esattamente gli stessi.

La seconda caratteristica riguarda come vengono selezionati i dati. È quello che abbiamo fatto con l’esempio relativo alla temperatura della superficie della Terra: a seconda del periodo preso si ottengono andamenti diversi. Selezionando opportunamente gli intervalli o rimuovendo alcuni dati, quindi, possiamo dare un’impressione piuttosto che un’altra. Tenete presente che la rimozione di dati può essere fatta “legalmente” senza che questo venga considerato un imbroglio. Ad esempio, si può sostenere che i dati che si discostano dalla media più di tanto potrebbero essere affetti da un errore sistemico e quindi giustamente scartati. È quello che si fa ad esempio con i voti della giuria in molte discipline sportive, come i tuffi dal trampolino o la ginnastica artistica, quando vengono scartati i voti più alto e più basso.

Terza caratteristica: i parametri di scala del grafico. Analizziamo ad esempio il livello di attenzione di un individuo impegnato in un’attività continuata di monitoraggio nell’arco della giornata. Se utilizziamo una scala stretta, ovvero ci concentriamo solo sui valori effettivamente misurati, noteremo molto bene una serie di picchi e di minimi che ci dicono come l’individuo in questione vari significativamente il suo livello di attenzione nell’arco delle 24 ore. Ma se gli stessi dati li rappresentiamo con una scala più ampia, ad esempio una che parta comunque da un livello zero di attenzione, ecco che avremmo l’impressione che tali variazioni siano semplici fluttuazioni di minor interesse. Qual è la verità?

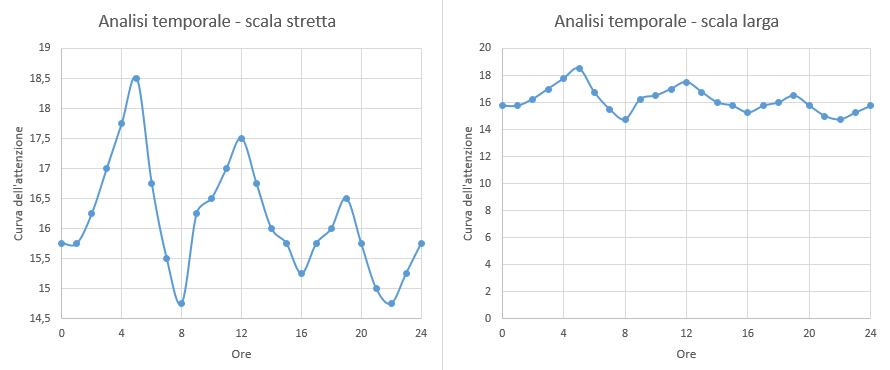
Ancora una volta non si può dire. Dipende se una variazione di attenzione di alcuni punti sia o meno significativa e questo non sono i dati a stabilirlo, ma la metrica utilizzata. In fondo nel grafico di destra il livello non cala mai neanche lontanamente verso lo zero; dobbiamo veramente preoccuparci per quell’andamento? Possiamo davvero dire che quella persona si sia periodicamente distratta o piuttosto il calo dell’attenzione misurato non è affatto rilevante?

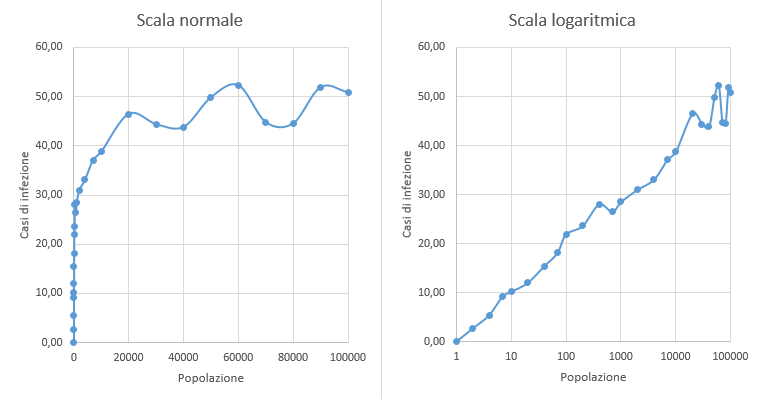
Un altro aspetto è relativo al tipo di scala utilizzata. Consideriamo lo stesso campione di valori e rappresentiamolo una volta con una scala normale e un’altra con una scala logaritmica. I grafici sembreranno molto differenti. La maggior parte della gente non è abituata a leggere i dati in scala logaritmica e quindi si può utilizzare questa tecnica per dare un’impressione di “crescita normale”, e di conseguenza non preoccupante, di dati che invece hanno un andamento esponenziale. Viceversa possiamo minimizzare dati che sono davvero preoccupanti.

Supponiamo ad esempio di voler rappresentare uno studio sull’incidenza di una certa malattia in base alle dimensioni dei vari centri abitati. Se usiamo una scala normale, la percezione sarà che nei piccoli abitati si ammalino in media circa 30 persone e che nelle grandi città si arrivi al massimo a 50, ovvero un numero di scarsa rilevanza su, magari, un milione di individui. Se però si usa una scala logaritmica ci si rende facilmente conto che se in effetti l’incidenza della malattia nelle grandi città è di scarsa rilevanza, nei paesini con una popolazione di 100 abitanti la percentuale di infezione è ben un quinto della popolazione, mentre nei casali e nelle fattorie il rischio che l’intera famiglia si ammali è elevatissimo. Ovviamente una malattia del genere non esiste, ovvero, questi dati sono del tutto inventati stavolta, ma questo esempio serve ancora una volta a evidenziare come i dati da soli non bastino. Per esempio, nel Paese in questione quante sono le grandi città? Dovessimo scoprire che sono solo due e che la maggior parte della popolazione vive nelle campagne in paesi e in villaggi al massimo di 200 persone, allora sì che ci sarebbe da preoccuparsi.

Un’altra caratteristica riguarda la rappresentazione del dato in termini di valore relativo o assoluto e rispetto a quale valore di riferimento. Consideriamo un altro dato molto discusso nel nostro Paese. Ancora una volta lo scopo non è quello di dimostrare una tesi, cosa che ormai avrete capito sia impossibile in base ai soli dati, ma di far vedere come rappresentando gli stessi dati in modo diverso, si possano sostenere tesi anche in antitesi fra loro. Ricordatevi tra l’altro, che qui vedete solo i dati che ho deciso di mostrarvi. Ma quali dati mancano? E quali altre considerazioni bisogna fare per interpretarli nel modo corretto?

Utilizzeremo i dati forniti dall’ISTAT per il periodo che va dal 2002 al 2012, ovvero:

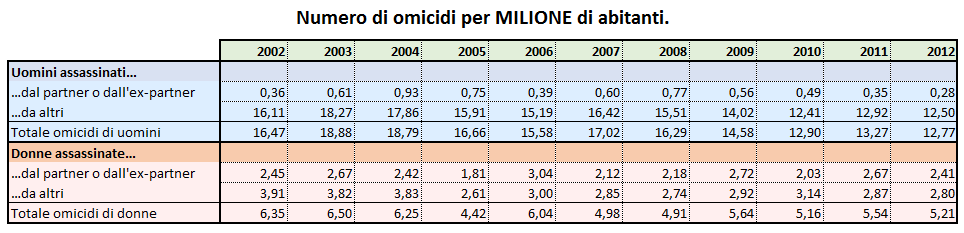
Proviamo a sviluppare, a partire da questi dati, un certo numero di grafici. Ricordate: i dati sono sempre gli stessi, solo i grafici cambiano.

Ragioniamo prima in termini di confronto per valori assoluti. Risulta abbastanza evidente come le donne siano principalmente uccise da partner ed ex-partner mentre gli uomini siano uccisi in prevalenza da altre persone. Inoltre i cosiddetti “femminicidi” sembrano essere decisamente più consistenti dei “maschicidi”, ovvero quei casi in cui il crimine è commesso da un partner o un ex-partner. La situazione è inversa nel caso di altre tipologie di assassini (parenti, amici, conoscenti, sconosciuti). In quest’ultimo caso il divario è ancora più consistente, questa volta a svantaggio degli uomini.

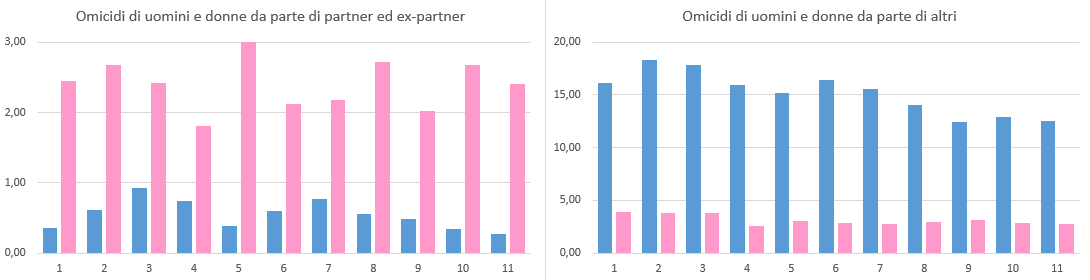
Se tuttavia ragioniamo per valori relativi e ci concentriamo sui rapporti uomini-donne nelle due tipologie di omicidi, i risultati hanno un aspetto totalmente differente, specialmente se usiamo un grafico ad andamento.

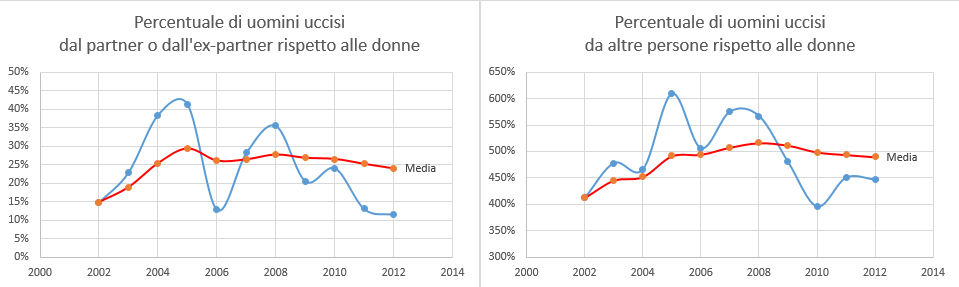
Nel primo caso, vediamo che in media, per ogni quattro donne uccise da un partner o un ex-partner, viene ucciso un uomo. Quindi i “maschicidi” sono il 25% dei “femminicidi”, con una punta di quasi il 45% nel 2005, dove si è sfiorato il rapporto di 2 ad 1. Viceversa le uccisioni dovute a parenti, amici, conoscenti o sconosciuti portano a una media del 500%, ovvero per ogni donna uccisa sono ammazzati 5 uomini, con un picco di questo rapporto che arriva nel 2005 a 5:1.

Perché è importante confrontare questi grafici? Perché i dati sono esattamente gli stessi, ma la percezione che possiamo dare a chi osserva i grafici può essere molto diversa nei due casi. Nel primo non c’è storia: sembra quasi che i “maschicidi” siano del tutto irrilevanti rispetto ai “femminicidi” e, analogamente, che quasi tutti gli altri omicidi vedano come principale vittima gli uomini. Nel secondo caso, in realtà, sembra che tutto sommato la percentuale di “maschicidi” rispetto ai “femminicidi” non sia poi così bassa, anzi, non si discosta di molto, con il suo 4:1, a quell’1:5 relativo agli omicidi da parte di altri.

Qual è la verità? In realtà non c’è nessuna verità. Almeno non qui. Ovviamente ce n’è una, ma va cercata in un’analisi ben più approfondita. Qui ci sono solo dati, che vanno contestualizzati per capirne il significato. Se non lo facciamo, si può alla fine sostenere qualsiasi teoria. Ad esempio, potremmo confondere ancora di più le idee se iniziassimo a vedere fra gli omicidi commessi da partner ed ex-partner, quanti di questi siano stati commessi dal sesso opposto e quanti da quelli dello stesso sesso, per poi normalizzare i valori dividendo rispettivamente per il numero di coppie eterosessuali e coppie omosessuali. Giocando su rapporti, percentuali, confronti, si possono creare curve di ogni forma a partire, ripeto, dagli stessi dati. Completando il tutto con affermazioni, frasi, foto, opinioni, nomi e tutte le altre tecniche che abbiamo visto nelle scorse puntate, si può portare l’opinione pubblica a pensare che ci troviamo di fronte a una situazione catastrofica come a far credere loro che il problema quasi non esista, a seconda di quale sia il nostro interesse.

Ovviamente su questi dati giocano poi altri fattori, come il “target” dell’articolo. Se sono donne, potrebbero reagire in un modo, se sono uomini in un altro, se sono donne o uomini che hanno subito effettivamente violenze in un altro ancora. Usando il canale giusto e quindi sapendo che si andrà a raggiungere un’audience specifica, si potranno rifinire i termini, le frasi, la forma dei grafici per ottenere le emozioni desiderate: rabbia, tristezza, senso di impotenza, indignazione, e via dicendo.

Un altro esempio è quello degli omicidi di massa con armi da fuoco negli USA. Qui l’obiettivo è quello di “dimostrare” che ci sono più omicidi negli USA a causa della maggiore facilità per i cittadini di possedere armi da fuoco. Bisogna capire quale sia il grafico più adatto per sostenere questa tesi.

I dati utilizzati sono veri e sono stati estratti da alcune tabelle presenti nella Wikipedia in lingua inglese. Per prima cosa scegliamo il tipo di grafico. Quello più adatto, dato che stiamo cercando una correlazione fra due fenomeni, è quello a dispersione.
Sull’asse X metteremo il numero di armi da fuoco possedute ogni 1.000 abitanti, sull’asse Y il numero di morti ogni 100.000 abitanti, in modo da avere un grafico più o meno quadrato. Notate il primo trucco: abbiamo parlato di omicidi di massa, i cosiddetti mass shooting, ma poi andiamo a usare nei grafici anche tutte le altre morti dovute ad armi da fuoco.

Consideriamo come dati di partenza tutti quei Paesi per i quali abbiamo entrambe le informazioni. In effetti i campioni relativi a ognuno dei due fenomeni considerati sono più ampi ma il problema è che solo per un certo numero di Paesi abbiamo entrambe le informazioni. Non si può fare altrimenti, onestamente, ma ecco che qui c’è già un altro inghippo. Sebbene perfettamente giustificato, non dare evidenza del fatto che mancano moltissimi Paesi, già vuol dire dare una percezione parziale del fenomeno nel suo complesso, presentata tuttavia come una fotografia globale, e quindi omnicomprensiva. Pochi infatti andranno a verificare quanti punti ci siano nel grafico e quali Paesi manchino, specialmente se ci sono tutti quelli più importanti e soprattutto quello del target che sta guardando il grafico.

Il grafico risultante è il seguente:

 

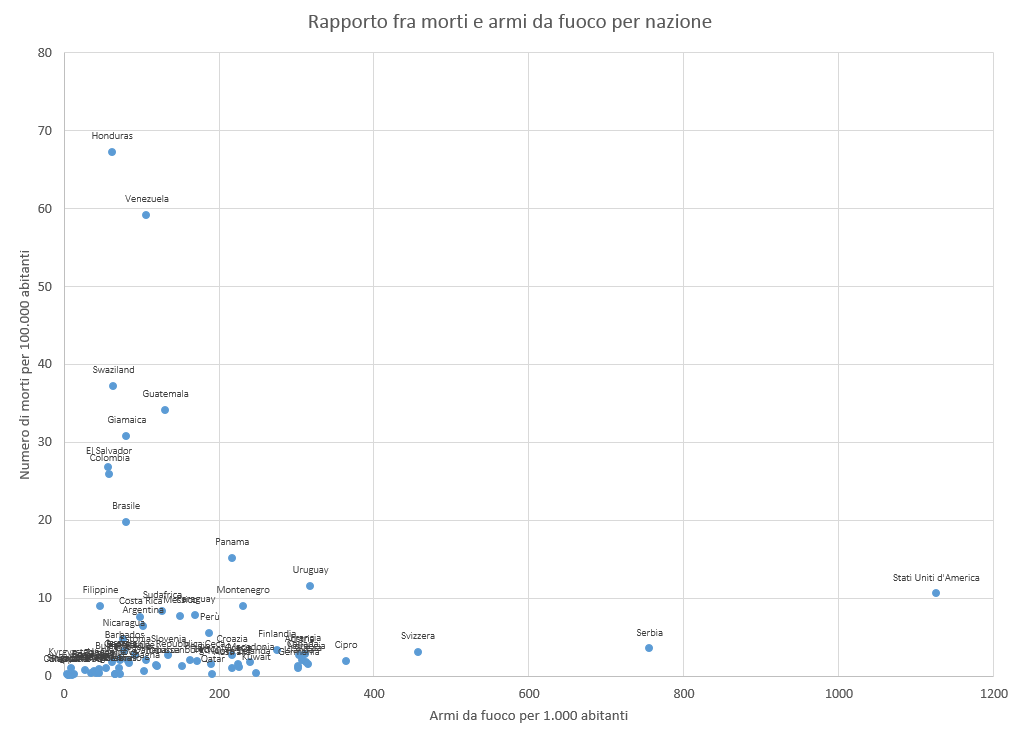
Come si può facilmente vedere, gli Stati Uniti hanno sicuramente il più alto valore di armi per abitante, ma non quello di morti a causa di armi da fuoco. Chiaramente questo grafico rende più arduo sostenere la tesi iniziale, ma se osserviamo quali siano gli Stati con un numero di morti ammazzati con armi da fuoco superiore a 20 ogni 100mila abitanti, vediamo che sono per lo più Paesi del Terzo Mondo. Abbiamo così trovato una scappatoia: ci basta infatti eliminare dal campione, a questo punto, i Paesi con un valore dello Human Development Index (HDI) inferiori a 0,79. Potremo sempre dire che stiamo cercando di fare un confronto fra Paesi “simili”, qualunque cosa questo voglia dire. Da notare che in questo modo eliminiamo anche il Brasile, che difficilmente si potrebbe far passare per un Paese del Terzo Mondo, ma che rappresenta comunque un dato “scomodo”. Il risultato è il seguente:

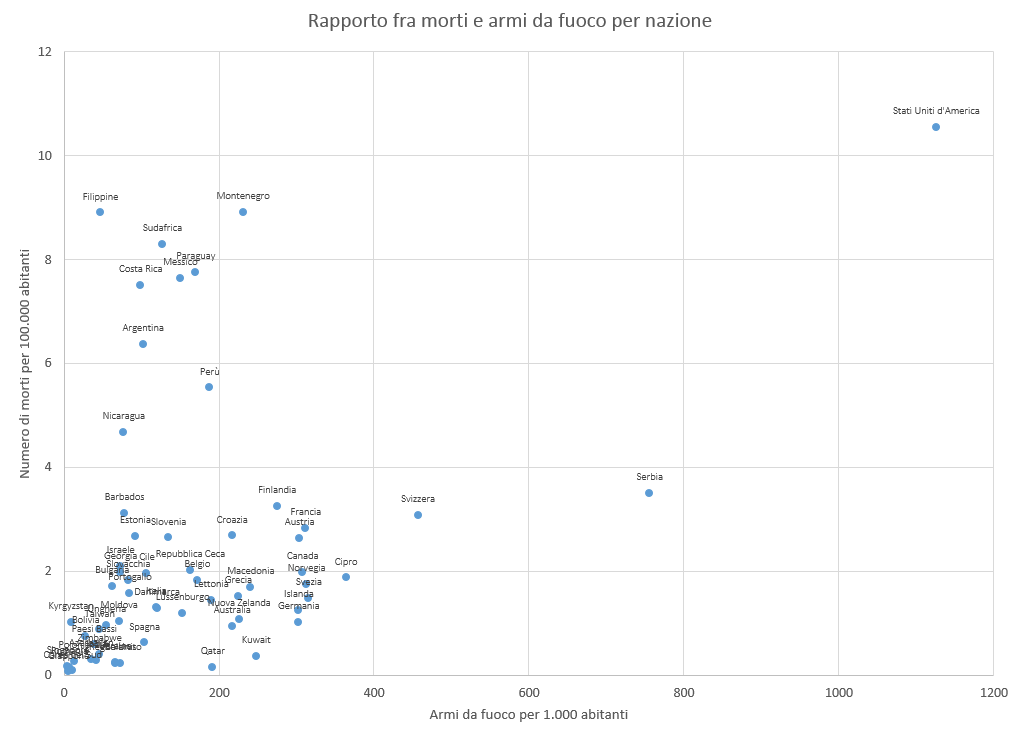
Va già molto meglio, perché abbiamo fatto schizzare gli Stati Uniti in alto a destra. In realtà in basso a sinistra abbiamo tenuto dei Paesi con HDI inferiore a 0.79 per fare “massa”, ma non lo diciamo, tanto le etichette si sovrappongono e difficilmente qualcuno lo noterà, specialmente se a questo punto evidenziamo con il colore rosso il Paese su cui vogliamo attirare l’attenzione e ci mettiamo pure una bella linea rossa a fare da separatore.
Il risultato finale è questo:

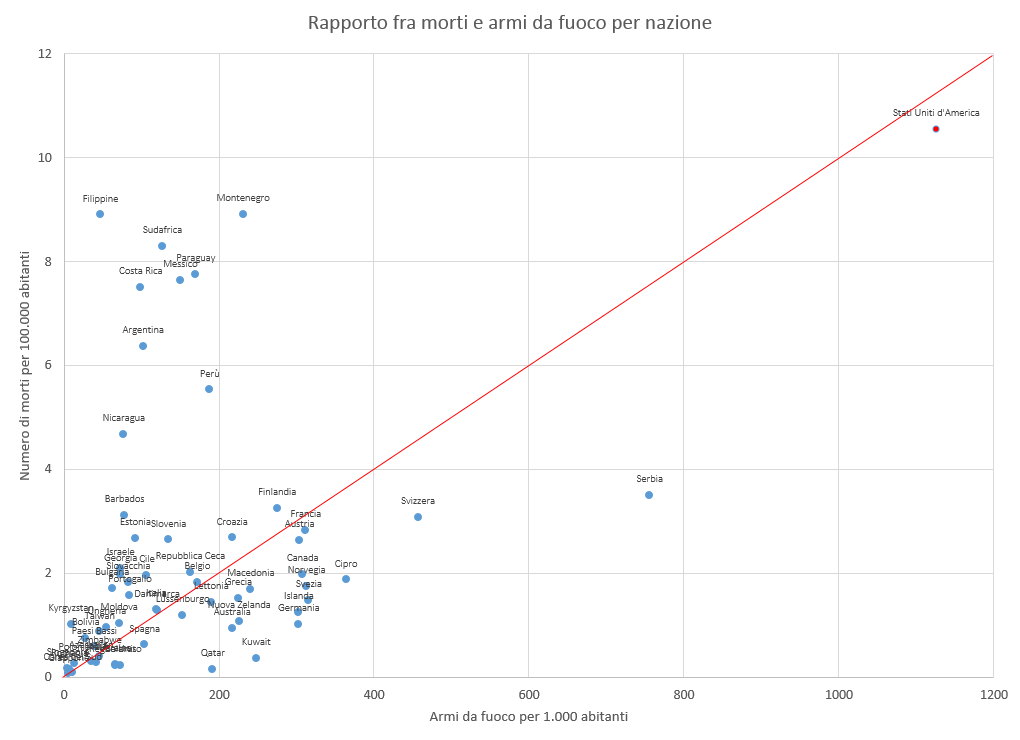
Da qui possiamo costruire un bell’articolo e “dimostrare” che negli USA i morti dovuti alle armi da fuoco sono di più perché è più facile acquistarle. Tenete presente che non si tratta di una tesi sballata: la facilità con la quale negli USA si possono acquistare e possedere armi da fuoco, anche molto simili a vere e proprie armi da guerra, è indubbiamente un fattore significativo e che contribuisce non poco all’elevato numero di morti causati da pistole, fucili e mitra in quel Paese. Ricordatevi che la disinformazione non dice mai davvero bugie, ma si limita a evidenziare alcune verità selezionate per manipolare la vostra opinione. Quindi la tesi è tutt’altro che falsa, però… Vediamo che succede se riportiamo lo stesso grafico mettendo sull’asse delle Y non tutti i morti causati da armi da fuoco, ma solo gli omicidi.

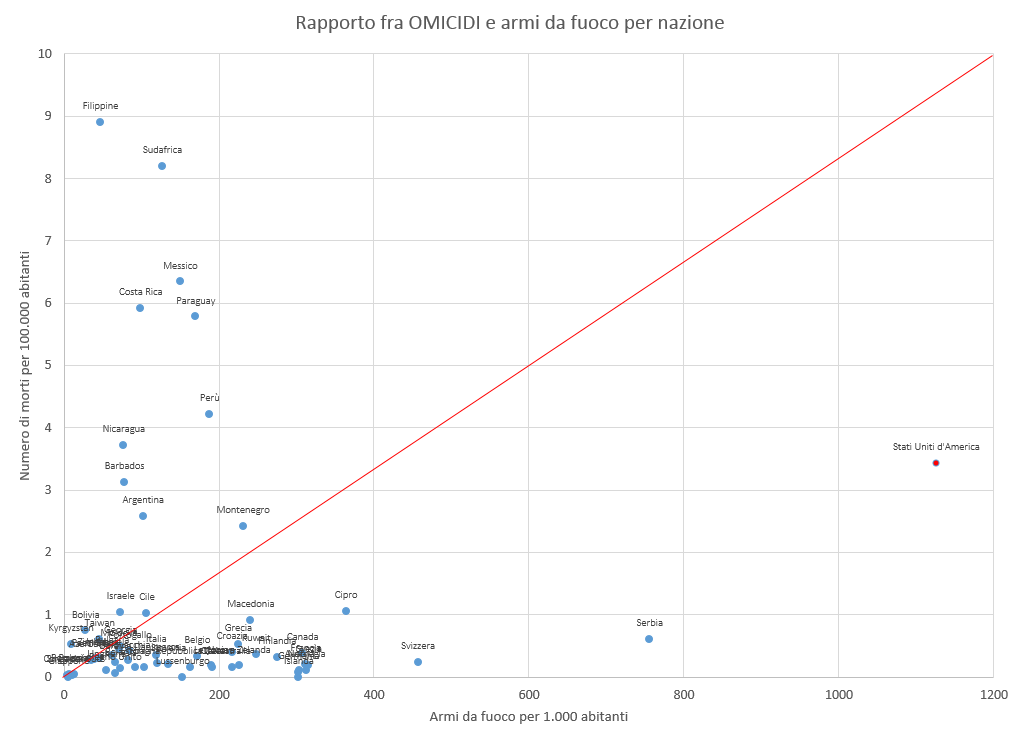
Sorpresa: gli USA crollano drasticamente rispetto ad altri Paesi. Come mai? Perché una buona parte dei morti statunitensi visti nel grafico iniziale sono in realtà… suicidi. Andiamo a riportare infatti lo stesso grafico solo per le morti dovute a suicidio commesso con un’arma da fuoco.

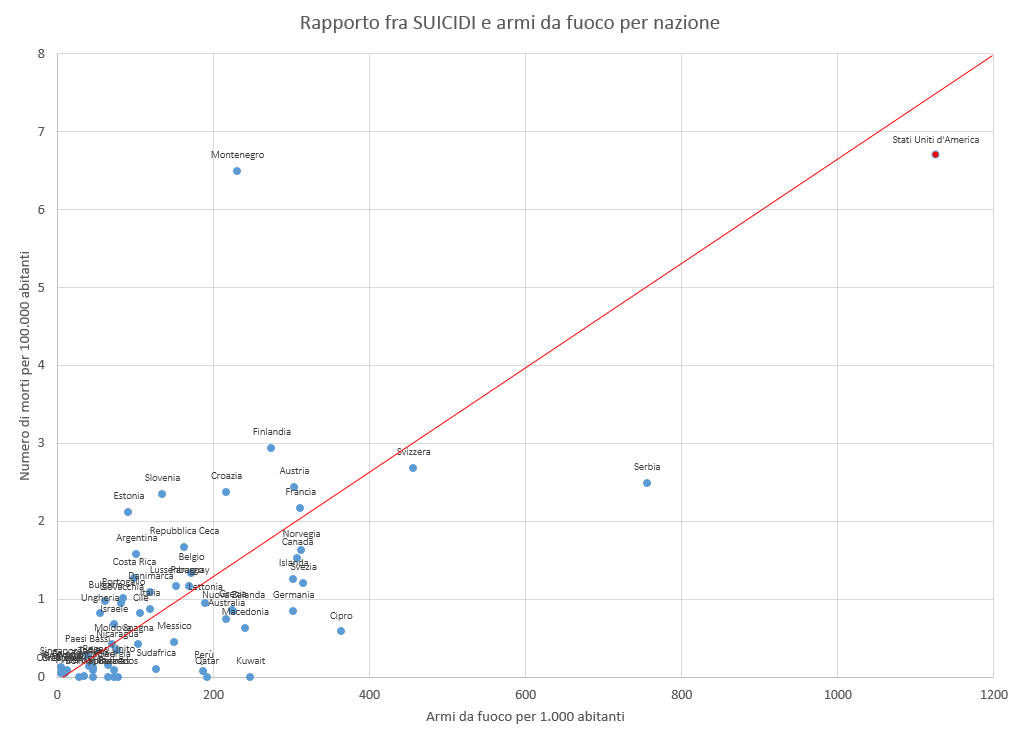
Ecco che gli USA tornano in cima alla classifica. Ovviamente potrei usare questo grafico per sostenere un’altra tesi, ovvero che la gente si suicida di più nei Paesi dove è più facile procurarsi delle armi, ma di nuovo starei sfruttando i dati a mio vantaggio. Vi ricordate della fatidica domanda “cosa manca” che ho detto bisogna sempre chiedersi? La risposta è semplice qui: “quanti sono i suicidi perpetrati con altri mezzi che non siano armi da fuoco nei vari Paesi del mondo?” Si può andare avanti per ore. A seconda del pezzetto che metto e tolgo posso rafforzare o indebolire qualunque teoria. Anche qui, solo uno studio approfondito può arrivare a una qualche conclusione attendibile, ma a noi non interessa. Il nostro scopo è disinformare, non informare.

Potrei fare molti altri esempi, ma rischiamo di andare troppo per le lunghe. Abbiamo visto qui anche l’uso di un’altra caratteristica di un grafico: lo stile. L’uso dei colori, come il rosso, per evidenziare, ad esempio, o le dimensioni dei caratteri. Il fatto che i nomi delle nazioni siano scritti molto in piccolo e che si sovrappongano fra loro e con i punti azzurri, rende confusa l’area in basso a sinistra che serve solo come “contrappeso” al Paese su cui voglio si concentri l’attenzione. Analogamente, l’utilizzo di elementi aggiuntivi per creare apparenti separazioni, aree, o altre zone su cui voglio si focalizzi lo sguardo, possono evidenziare alcune parti del grafico e far passare inosservate altre.

Ricapitolando, mostrare un grafico è uno dei sistemi principi per fare disinformazione. Ovviamente è fondamentale che i dati siano veri e possibilmente da una fonte attendibile. Dopodiché basta giocare sulla selezione all’interno del campione, sul tipo e sulle varie caratteristiche del grafico, sullo stile grafico e su una serie di elementi aggiuntivi che posiziono strategicamente, per raggiungere il nostro scopo.

Provate a farlo davvero, provate a immaginare una tesi assurda e poi a usare dati reali per sostenerla. In rete si trovano dati di tutti i tipi. Partite sempre dai valori numerici, mai dai grafici disegnati da altri. Con un po’ di pazienza vi accorgerete di quanto sia facile ottenere determinati risultati.
Sarà un esercizio molto educativo, soprattutto se pensate che se è facile per voi, cosa possano davvero fare gli esperti di disinformazione.

Buon divertimento.

de Judicibus